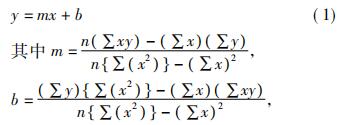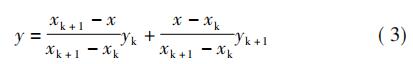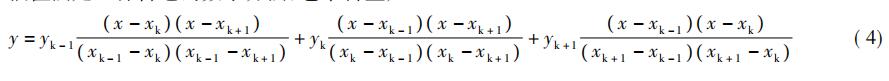摘要:依托建立的低温精馏装置,针对低温环境中温度测量问题,提出一种基于LabVIEW的低温温度测量方法。该方法将插值法引入到数据分析中,通过软件编程实现数据处理、显示、存储等功能。经过理论分析与实验对比,该方法准确度提高到0.01K,可移植性强,是低温环境中温度测量的可行方法。
引言
低温技术不仅涉及医疗、农业、生物学等与人们生活息息相关的行业,越来越多的尖端科学领域也与其密不可分。而低温温度的测量是低温物理实验中首要和非常基本的测量。随着新型温度计的不断研制和测量方法的不断增多,准确程度也逐渐提高,测量的温区不断向更低温度延伸。实际应用中所能达到的测温精度,很大程度取决于
温度计的合理使用和安装,以及仪器仪表的正确使用[1]。由低温温度计在整个测量温区是非线性的,因此其分度表越详细,则仪器测量的准确度越高。低温温度值的测量一般可通过两种方式实现,一是通过温度变送器,无需编程,只需在变送器里设置温度计类型与标定的分度值,仪表即可显示实际温度值,另一种方式是通过高精度的数字电压采集仪表,采集低温温度计的电阻或电压信号,然后按照分度表进行转换,显示温度值[2]。方法一变送器对于标定值即温度参考点的设定个数有数量限制,实际应用中只能选择工况附近温区的标定值,以提高测量精度;方法二需依靠软件编程,对于分度表数量不限,可保证全量程的测量精度。
本文利用方法二,依托现有的低温精馏装置,将曲线拟合的插值法引入测量过程,应用Lab-VIEW软件实现该方法的软件编程,并分析对比此方法对测量结果的影响。
2测量硬件组成
实验室建立的低温精馏装置安装的是铑铁电阻温度计,分度温区范围为1.2~300K,准确度为0.01K。低温试验中,温度计引线一般又细又长,且须通过温度梯度很大的区域,因此引线电阻较大且不够稳定,甚至比测温元件的阻值还大很多。为消除引线电阻的影响,电阻元件通常用四根引线,将电流引线和测量电压的引线分开,即采用四引线电位法进行测量[3],温度计安装时须做好热接触和绝缘。测量仪表选择具有七位半精度的数字电压表,26位分辨率,远程接口包括GPIB、USB和以太网,主机包括六个插槽,每个插槽可实现60路差分测量或30路四线制测量。利用工控机通过以太网与数字电压表进行通讯,按照既定程序运行,具体控制系统硬件见图1。
3测量方法
数字电压表采用四线制接法,测量温度计的电阻信号,根据每只温度计的分度表按照一定运算方法进行转换,得到实际温度值,温度计的分度表见图2。
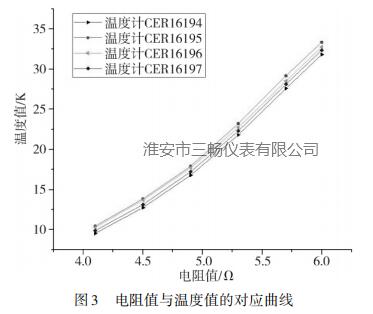
根据分度表可得到电阻值与温度值的对应曲线,将温度计正常工况下用到的温区进行放大,如图3所示。由图可知,四支铑铁温度计的电阻值与温度值并非线性对应关系。数字电压表实时采集铑铁温度计电阻值,按照电阻值与温度值的对应曲线求出当前的温度值。
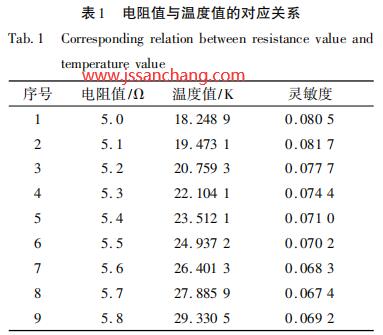
根据温度计的分度表,用函数y=f(x)来表示某内在规律的数量关系,分度表仅给出一定范围内一系列点xi的函数值yi=f(xi),其中i=0、1、…、n,而实际应用中往往需求出表上未包含的函数值,因此该过程可看作是曲线拟合过程。本文应用插值法和非常小二乘法来求解拟合问题,并对结果进行分析,表1给出了分度表中部分电阻值与温度值的对应关系,其中灵敏度是指电阻随温度的变化率,即电阻变化率除以温度变化率。
首先,应用曲线拟合的非常小二乘法,该方法在应用科学中具有重要作用,它是离散点的非常佳平方逼近。用非常小二乘法求拟合曲线时,首先要确定S(x)的形式。根据表1的数据分析,设定拟合公式为:
由表1可知,n=9。经计算可得m为14.044827、b为-52.203141,于是得到公式:y=14.044827x-52.203141(2)将实测的电阻值带入式(2),即得到温度值。其次,应用拉格朗日一次插值多项式进行计算。插值法是一种古老的数学方法,它来自生产实践,基本理论和结果是在微积分产生后才逐步完善,其应用也日益增多,特别在计算机广泛使用后,由于航空、造船、精密机械加工等实际问题的需要,插值法在实践上及理论上显得更为重要,并得到进一步发展[4]。拉格朗日一次插值多项式为:
实际应用中,实测电阻值为x,选择分度表中和实测电阻值非常为相近的两个点xk和xk+1,带入式(3),可得当前温度值。非常后,应用拉格朗日二次插值多项式进行计算,插值公式如下:
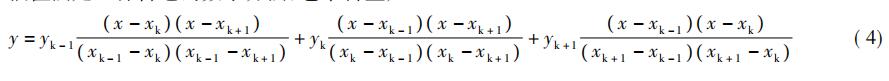
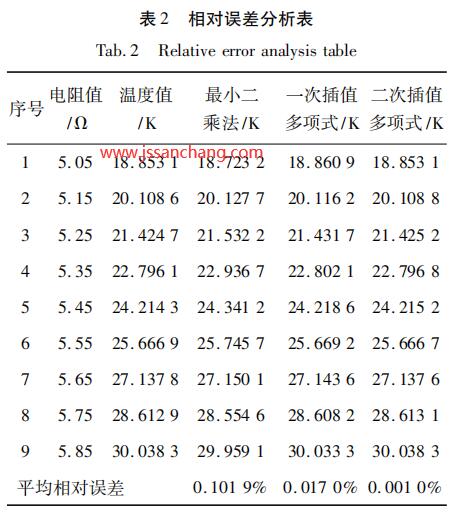
假设实测电阻值为 x,选择分度表中和实测 电阻值非常为相近的三个点分别为 xk - 1、xk和 xk + 1 ,带入式( 4) ,可得温度值。 综上所述,取 9 组数据分别用以上三种方法进行计算,对相对误差进行分析对比,如表 2 所 示。应用拉格朗日二次插值多项式进行计算的相 对误差非常小。将标准值与用二次插值多项式方法所得测量值比较,测量的准确度达到 0. 01 K,满 足设计要求。
4 软件编程
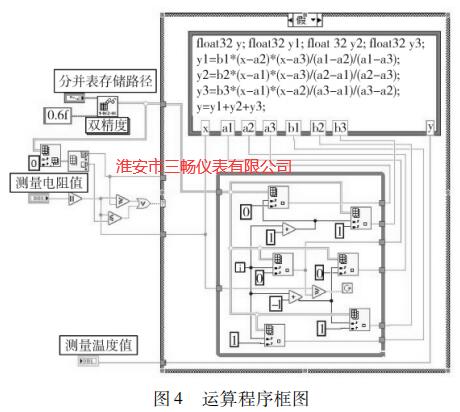
随着测试和计算机技术的发展,虚拟仪器获 得了更为广泛的应用,它实际上是一个按照仪器 需求组织的数据采集系统,利用计算机的强大功 能和丰富资源,在相应测试软件的配合下,可灵 活高效地开发仪器系统。目前这一领域,使用较 广泛的计算机语言是美国 NI 公司的 LabVIEW, 它包括齐全的用于数据采集、分析、显示、存储数 据、调试代码等工具[5,6]。确定使用拉格朗日二次插值多项式算法后,可使用 LabVIEW 来实现该运算过程,其运算程序框图如图 4 所示。
5、结论
本文利用实验室建立的低温精馏装置,针对低温环境中温度测量问题,提出了一种基于 Lab- VIEW 的低温温度测量方法。此方法是将数值分 析中的插值法引入到数据分析中,并通过软件编程实现数据处理、显示、存储等功能。经多种方法 的理论分析与实验对比,应用二次插值多项式方 法所得的测量值准确度达到 0. 01 K。该方法可移植性强,为低温环境中的温度测量提供了有益参考。