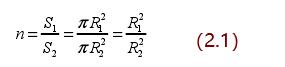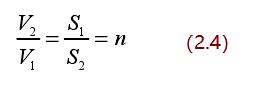缩径式涡街流量计的缩径结构
图 2.1 是缩径式涡街流量计的缩径结构的示意图,它包括收缩段、稳定段、测量段。稳定段是收缩段入口前的大口径管道,测量段是收缩段出口后的小口径管道,发生体和传感器安装在测量段。
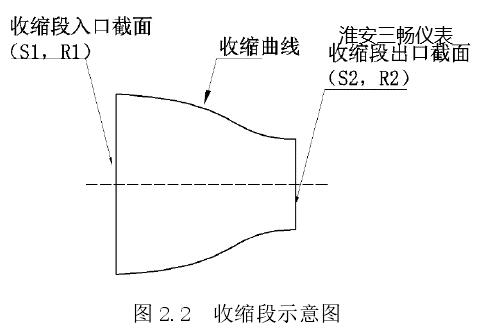
收缩段是缩径结构的重要组成部分,图 2.2 是收缩段的示意图。收缩段由收缩曲线和收缩比两部分组成。收缩曲线是指从大管径过渡到小管径的壁面线条。收缩比是收缩段入口截面面积与出口截面面积之比,其计算公式如下:
式(2.1)中,n 是收缩比,S1 是收缩段入口面积,R1 是收缩段入口截面半径,S2是收缩段出口面积,R2 是收缩段出口截面半径。
流体的连续性定理描述了流体流经不同截面的管道时流速与截面面积的关系,其内容是:当流体连续不断地流过管道,单位时间内流过管道各个截面的流体的体积或质量都相等。这一定理可用式(2.2)表示:
A1v1 =A2v2 (2.2)
式(2.2)中,A1是流体流入截面的面积,v1 是流体在流入截面时的速度,A2是流体流出截面的面积,v2 是流体在流出截面时的速度。
收缩段中的流体同样满足连续性定理。假设收缩段入口截面上的流体流速为V1,收缩段入口截面的面积为 S1,收缩段出口截面上的流体流速为 V2,收缩段出口截面面积为 S2,有:
S1V1 =S2V2 (2.3)
联立式(2.1)、(2.3)可得:
可知,流体在收缩段出口的流速是其在收缩段入口流速的 n 倍,n 即是收缩段的收缩比。这也是缩径式涡街流量计使小流量变大,实现宽量程比的理论基础。