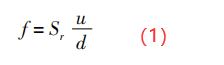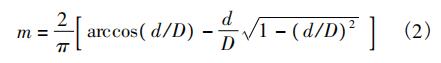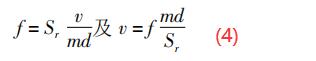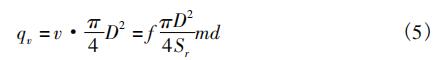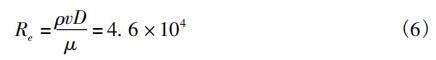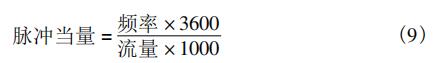0、引言

      Ｒoshko于1954年首次提出用卡门涡街现象进行流量测量，期间经过很多学者的实验研究和理论分析，逐渐发展成工业实践中使用的智能涡街流量计;［1］自20世纪60年代末开始研制以来，涡街流量计发展非常迅速，可适用于液体、气体、蒸汽，是一种比较先进、理想的流量仪表。［2］本文将先通过实验对在不同流体条件下的相对示值误差进行分析，再利用SOLIDWOＲKSFLOWSIMU-LATION流体计算软件对涡街流量计进行相应的流场分析等。

 

1涡街流量计结构及流量测量原理

1.1涡街流量计结构

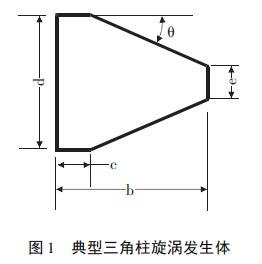
      旋涡发生体(阻流件)是涡街流量计的核心部件，它的主要功能是把三维的流体变成二维的旋涡流;其结构形状非常基本的是圆柱型、三角柱型和矩形柱，其他的形状皆为这些基型的变形。现在经过大量的实验和现场使用，非常为流行的是三角柱和三角柱的变形梯形柱［7］(如图1所示)，结构参数之间的关系一般存在d/D=0.2～0.3、c/b=0.1～0.2、b/d=1～1.5、θ=15°～65°;［8］其优点是能产生规律较好的涡街、斯特劳哈尔数Sr线性度较高。

1.2测量原理

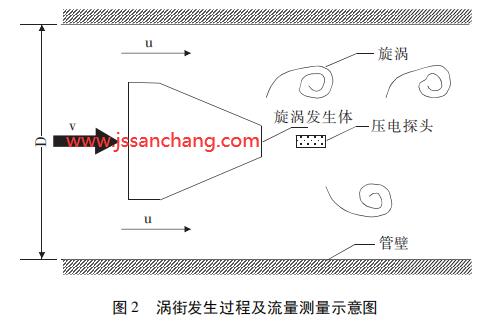
      涡街流量计利用卡门涡街原理，即流体流经流量计时，在旋涡发生体下游两侧交替地分离释放出两列有规律的交错排列的旋涡(如图2所示)，在一定雷诺数范围内，该旋涡的频率与发生体、管道的几何尺寸有关，旋涡的频率正比于流量，此频率可由探头检出。

      当涡街稳定时，旋涡释放频率f与流经旋涡发生体两侧的平均流速u之间的关系可表示为:

      式中:f———旋涡频率，Hz;Sr———斯特劳哈尔数，雷诺数Ｒe在3×102～1.5×105的范围内，Sr———常数;

            u———旋涡发生体两侧流体的平均流速，m/s;

            d———旋涡发生体迎流面的宽度(如图1所示)，m。

      设测量管内径为D(如图2所示)，发生体两侧弓形流通面积之和与测量管的横截面积之比为m，则:

      根据流体连续性方程:v=u·m(3)

            式中:v———测量管内流体的平均流速，m/s。

      将式(3)代入式(1)，得:

      设测量管内的瞬时体积流量为qv，m3/s;则:

      因此，对确定的测量管内径D和旋涡发生体迎流面宽度d，流体的瞬时体积流量qv与旋涡频率f成正比;只要测得旋涡频率f，就可测量出体积流量qv的值。

 

2实验

2.1实验材料

      本文实验对象为江苏杰创科技有限公司生产的DN100、编号为JC180335的三角柱型涡街流量计，流量范围是(0.0～100.0)m3/h，1.5级，实体结构及主要参数如图3所示。

      使用的标准装置为标准表法水流量标准装置，0.2级，流量范围(5～2200)m3/h、适用口径DN(50～500)mm，实验管道为DN100，数据输出模式选择(4～20)mA电流输出;如图4所示进行涡街流量计现场实验，前后直管段满足测量要求。

2.2实验方法

      经现场实验发现:当管道内设定流量低于10m3/h时，涡街流量计的电流输出为0mA(表头显示0.000m3/h);调节阀门开度，逐步增大流量点至13m3/h时，数据输出正常。根据研究对象的流量范围，选取13m3/h、20m3/h、50m3/h、80m3/h等为流量参数采用标准表法在不同介质压力下进行相对示值误差计算。

 

3实验结果及分析

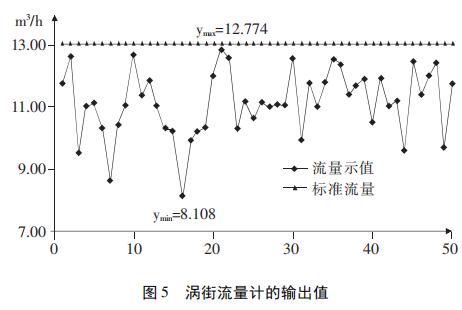
3.1调节阀门的开度及泵的频率使得管道流量达到被检涡街流量计的有效下限值13m3/h，记录下此时涡街流量计的输出值(共计50个数据);如图5所示，数据不稳定，非常小值、非常大值分别为8.108m3/h、12.774m3/h，经格拉布斯准则［12］判定均不是异常值;经计算得到相对示值误差E=－14.44%，标准偏差σ=8.05%。

      导致流量输出不稳定，造成相对示值误差及重复性偏大的原因可能是:液体介质流量过低(下限有效流量)，致使雷诺数偏低;根据文献［3］得知:20℃水的动力粘度μ=1.003×10－3Pa·s、密度ρ=998.2kg·m－3，此时13m3/h对应的来流速度v=0.46m/s，流场的特征直径D=0.1m;根据式(6)得:

      由文献［9］可知:对于多数涡街流量计，雷诺数Ｒe在2×104～7×106范围内(可见Ｒe=4.6×104在下限附近)Sr可看为常数，可保证测量的准确度;超出该范围，Sr将随Ｒe的降低或升高而变化，涡街流量计将出现非线性，从而导致涡街流量计的准确度会降低。另外，管道内介质的压力也可能会造成涡街流量计的准确度降低，在后续实验中，将进行同一流量点、不同介质压力下进行相对示值误差实验。

 

3.2调节阀门的开度及泵的频率使得管道流量达

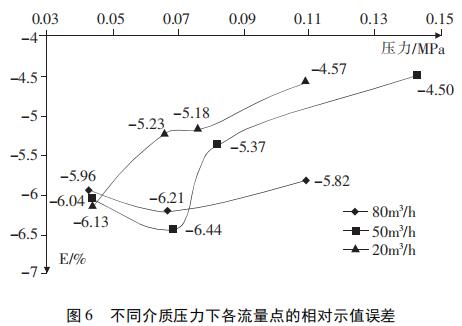
      到设定的流量值20m3/h、50m3/h、80m3/h，调节管道内的介质压力;记录不同管道介质压力下涡街流量计的输出值，并进行相对示值误差计算。

 

      如图6所示，相同流量点、不同介质压力下的相对示值误差不同，且随着压力的增大，相对示值误差均有不同程度上升的趋势，中、小流量点下表现得尤为明显;相对应的大流量点下的相对示值误差对压力变化略显得不太敏感。整体来说，分界流量0.2qmax以上各流量点对应的相对示值误差还是呈线性的，可以通过调节流量传感器系数(Sensor－Factor)进行校准;另外在今后进行涡街流量计中、小流量检测时尽可能的增大管道内介质的压力等。接下来进行涡街流量计三维建模及流场仿真分析，进一步研究不同流体条件下涡街的工作原理等。

4CFD仿真分析与探讨

4.1建立模型

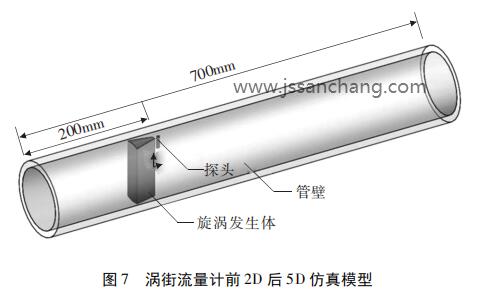
      应用CAD软件SolidWorks依据上述涡街流量计的内部实际尺寸建立计算区域模型，为了尽可能降低网格数、提高仿真计算效率，采用根据前2D后5D的直管段安装要求建模，如图7所示。

4.2网格划分

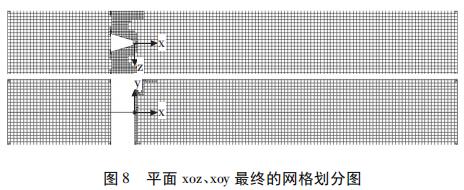
      选择自动网格划分，初始网格划分级别选择6，非常小缝隙尺寸即为旋涡发生体与探头之间的距离5mm，其余选择默认状态，运行网格求解得到模型总的流体网格数为197894，其中，接触固体的流体网格数为59948，如图8所示。

4.3求解设置

      分析类型选择内部流场分析，并排除不具备流动条件的腔;重力加速度方向选择y轴负方向、g=9.81m/s2;涡街流量计的内部流场为非定常流，选择瞬态分析，设定仿真时间10s、保存间隔周期0.05s;流体介质选择水，其密度为998.2kg/m3、运动粘度为1.003×10－3Pa·s;流动类型为层流和湍流;初始条件x方向速度为0.46m/s(即13m3/h)，湍流参数选择湍流强度和湍流长度，其中湍流的定义方法选择湍流强度I［13］(见式7)和湍流长度I［14］(见式8)，经计算当v=0.46m/s时湍流强度I=4.18%、I=0.007mm。

      选择速度、压力及力作为全局目标，选取探头表面一侧(z正方向)表面受到的力为表面目标，然后运行求解。

 

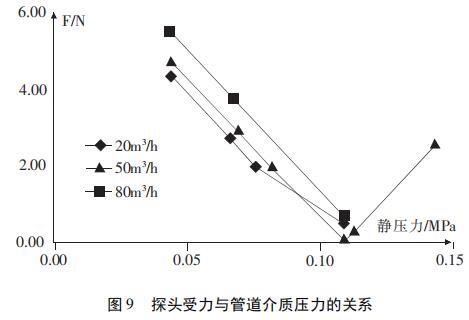
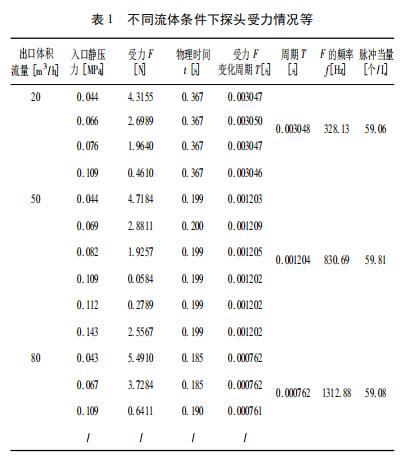
      通过分析表1数据得出同一流量点下，管道内介质压力不同，探头受力是不一样的，且在管道介质压力小于0.1MPa时，各流量点下随着管道压力的增大，探头受力变化趋势一致，均是逐渐减小，如图9所示;以流量点50m3/h为例，继续增大管道内介质压力，发现在管道压力大于0.1MPa的条件下，探头受力F随流量点的增大呈增大趋势。

      从涡街流量的工作原理和仿真数据知道，探头的受力是周期性的，随着流量点的增大探头受力周期呈减小趋势;且周期的大小与管道内的介质压力无关，只与介质流量的大小有关，通过周期的倒数可得到不同流量点下的探头受力的频率大小，即探头受力的频率与介质流量呈正相关，如图10所示。结合式(9)可计算得到基于探头受力条件下的脉冲当量，结果发现脉冲当量(60个/L)是一个定值，与管道压力、介质流量无关等。

      式中:脉冲当量单位为个/L;频率的单位为Hz;流量的单位为m3/h。

4.4仿真结果与分析

      在实际的检校验工作，同一个直管段只有一个入口和一个出口，则可认为入口流量与出口流量相当，为了研究介质压力的单因素变化对探头受力的影响，在仿真的初始条件分别根据实际数据设置出口速度和入口静压力，仿真结果如表1所示。

5结论与探讨

5.1结论

      本文阐述了涡街流量计的工作原理。通过实际实验得到涡街流量计存在有效下限值(分界流量以下)，在该流量值下存在较大相对示值误差，且重复性不佳;在分界流量以上，相同流量点随着压力的增大，相对示值误差均有不同程度上升的趋势，中、小流量点下表现得尤为明显，大流量点下的相对示值误差对压力变化略显得不太敏感;整体来说，分界流量0.2qmax以上各流量点对应的相对示值误差还是呈线性的。通过仿真模拟发现当管道介质压力小于0.1MPa时，随着介质压力的增大探头受力变化趋势一致，均是逐渐减小，当管道压力大于0.1MPa的条件下，探头受力F随流量点的增大呈增大趋势;另外，探头的受力是周期性的，随着流量点的增大探头受力周期呈减小趋势，只与介质流量的大小有关，与管道内的介质压力无关，通过周期的倒数可得到不同流量点下的探头受力的频率大小，即探头受力的频率与介质流量呈正相关。

 

5.2探讨

通过实验及仿真模拟引发一些思考，也是今后进一步研究涡街流量计的方向:

      (1)涡街流量计工作原理中提到的旋涡频率与本文中仿真得到探头受力频率之间存在什么样的关系。

      (2)由仿真模拟，根据探头的受力频率换算得到恒定的脉冲当量(60个/L)与实际工作条件下脉冲当量是否一致。

      (3)卡门涡街的形成与雷诺数有很大的关系，根据雷诺数计算公式，其值与管道介质压力无关，与仿真得到的探头受力大小与管道介质压力存在强的相关性是否矛盾。